К.э.н . Тимченко А.Б., Тимченко О.В., Горбаченко В.А.

Северокавказский федеральный университет, г. Ставрополь , Российская   Ф едерация

К ВОПРОСУ О ПРОГНОЗИРОВАНИИ С ПОМОЩЬЮ АДАПТИВНЫХ ПОЛИНОМОВ ЛАГЕРРА

 

Специфика прогнозных задач в экономике, прежде всего, определяется сложностью и динамичностью протекающих в ней процессов. Оставляя неопределенной сущность своей реальности в прошлом, эти процессы тем самым исключают возможность перенесения прошлых закономерностей на будущее. В подобных ситуациях практически единственный подход, который может привести к успеху, основан на принципах адаптации.

Первые модели адаптивного прогнозирования были разработаны для одномерных временных рядов, применение к которым традиционных методов было не совсем корректным. Наиболее известными адаптивными моделями для одномерных временных рядов являются предиктор Хольта и адаптивный полином Брауна. Эти модели, безусловно, позволяют достичь высокого уровня адекватности при моделировании довольно сложных закономерностей развития экономических процессов. Но еще более широкими возможностями обладает предложенная Р. Брауном обобщенная модель, представляющая собой линейную комбинацию известных детерминированных функций от времени  

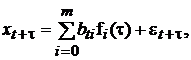                            (1)

где – моделируемый показатель; – ненаблюдаемая случайная величина

В качестве   чаще всего используются полиномы. Например, в простейшем случае можно принять , ,   и т.д. Для обновления коэффициентов адаптивной модели разработана компактная рекуррентная схема в предположении, что функции   удовлетворяют соотношению

        (2)

  где   вектор-столбец из функций, входящих в модель; – матрица постоянных коэффициентов размерностью   называемая матрицей перехода.

Соотношение (2) позволяет по вектору начальных значений и матрице   получить значения   для любого момента времени  

.          (3)

Для упрощения расчетов за начало отсчета времени принят текущий момент времени   и, следовательно, все функции модели имеют отрицательный аргумент. В качестве критерия минимизации ошибки аппроксимации используется взвешенная сумма квадратов отклонений

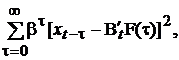        (4)

где – вектор текущих параметров модели; – параметр сглаживания ( ).

Если ввести в рассмотрение диагональную матрицу весовых коэффициентов с элементами   и матрицу

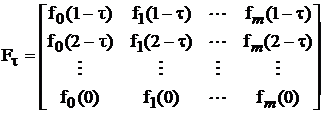,       (5)

то выражение для , при котором достигается минимум (4), можно записать в виде

            (6)

где

После некоторых преобразований, используя матрицу перехода , можно записать рекуррентную формулу для адаптивного обновления коэффициентов полинома (1)

       (7)

Важное для вывода рекуррентной формулы соотношение (2) выполняется для функций, которые являются решениями линейных разностных уравнений. C реди функций подобного рода идеальными для обобщенной модели Р. Брауна являются дискретные полиномы Лагерра , которые в силу свойства ортогональности с весом значительно упрощают рекуррентную формулу (7).

Пусть используемые в модели (1) функции   являются полиномами Лагерра . Известно, что они могут быть записаны в виде

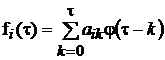,    (8)

где   , .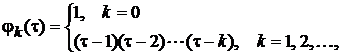

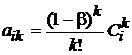Для наглядности покажем, как записываются полиномы трех первых степеней

, , ,

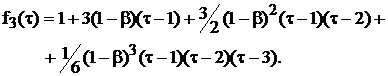     (9)

Полезное для упрощения свойство ортогональности этих полиномов выглядит следующим образом:

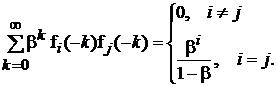        (10)

Левая часть записанного выражения представляет собой элемент матрицы , стоящий на пересечении - й строки и -го столбца, т.е.

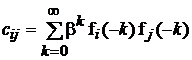.            (11)

Следовательно, если в качестве функций   выбираются дискретные полиномы Лагерра , то матрица   диагональная с элементами, рассчитываемыми по формуле (11).

Матрица перехода для полиномов Лагерра также имеет довольно простую треугольную структуру. Ее элементы определяются выражением

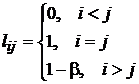.             (12)

Свойство ортогональности и треугольная структура матрицы перехода совместно с тем, что для полиномов Лагерра

,   (13)

              (14)

позволяют переписать рекуррентную формулу (7) в виде

,           (15)

где , а   – ошибка предсказания на один шаг вперед, представляющая собой разность вида

           (16)

Полученное для обновления коэффициентов предсказывающего полинома выражение (16) имеет довольно простую структуру, которая не зависит от степени полинома, что делает возможным одновременный расчет прогнозных значений по полиномам различных степеней. Эти свойства упрощают процедуру выбора оптимальной степени полинома и, кроме того, делают сам метод удобным для программной реализации.