К. х. н. Каримова Л. М., Кайралапов Е. Т.

ТОО «КазГидроМедь» «НИЦИТ», г. Караганда, Республика Казахстан

О ВОЗМОЖНОСТИ ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ МОДЕЛИ ИЗМЕЛЬЧЕНИЯ С ИСПОЛЬЗОВАНИЕМ ЗАБАЛАНСОВОЙ МЕДНОСУЛЬФИДНОЙ РУДЫ ЖЕЗКАЗГАНСКОГО МЕСТОРОЖДЕНИЯ

В работах [1–4] на основе подобия процесса измельчения в водопадном режиме работы шаровых барабанных мельниц и химических процессов для последовательных реакций разработана вероятностная теория процесса, подчиненная единому наиболее общему выражению скорости процесса через частотный ( Z ), стерический ( Р _ст ), активационный ( Р _а ) и концентрационный ( Р _конц. ) факторы. Уравнение для константы скорости процесса измельчения имеет вид

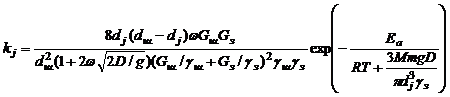, (1)

где ω – частота вращения мельницы, с ^-1 ; D – внутренний диаметр мельницы, м; g – ускорение силы тяжести, м/с ² ; d _j – средний размер зерен фракции с индексом j в порядке уменьшения размера, м; d _ш – диаметр мелющего шара, м; Е _а – энергия активации измельчения, Дж/моль; М – молекулярная масса самой твердой составляющей зерна (обычно, кварца), кг/моль; m – масса мелющего шара, кг; γ _з – плотность руды (зернового материала), кг/м ³ ; R – универсальн ая газовая постоянная, Дж/(моль·К); Т – абсолютная температура (обычно принимаемая равной 298 К); G _з – масса руды в мельнице (зерен), кг; G _ш – масса шаров в мельнице, кг; γ _ш – плотность шаров, кг/м ³ ; Р _j – долевое содержание фракции со средним размером зерна d _j .

В свою очередь, эта константа вводится в интегральную модель измельчения, учитывающую не только убыль содержания каждой фракции, но и прирост его (кроме первой фракции) за счет образования осколков от предыдущей фракции в строгом соответствии с кинетикой последовательных химических и физических превращений [1–4]:

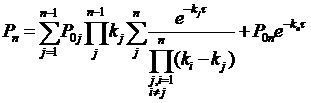, (2)

где n – номер рассчитываемой фракции, j – номера предыдущих фракций и соответствующих стадий разрушения зерен, P _0j – исходное долевое содержание фракций, τ – продолжительность измельчения, с.

Эта формула была применена на модельных примерах для анализа всех особенностей измельчения, ранее не имевших строгого теоретического обоснования. Вместе с тем, судя по выражению константы скорости (1), данная модель применима только к описанию сухого измельчения, так как учитывается объемы только шаровой загрузки ( G _ш /γ _ш ) и рудного материала ( G _з /γ _з ), вместе дающие по долевому распределению единицу

(3)

Между тем в настоящее время большинство процессов измельчения в барабанных мельницах реализуются в условиях мокрого измельчения, т. е. в присутствии воды, причем в весьма заметных количествах. О влиянии разбавляющего действия для выражения долей шаров и зерен лишь упомянуто в работе [4], но не доведено до формального выражения, хотя это должно отражаться и на абсолютном долевом содержании фракций в смеси шаров, руды и воды, а также взаимодействия этих фракций с мелющими телами.

Это влияние можно формализовать по подобию учета объема растворителей в химических фракциях, тем самым сохраняя общий подход к отображению химических и механических процессов превращения вещества, использованный в [1–4]. Для этого достаточно выразить общий объем системы через сумму ее составляющих с учетом объема воды в мельнице (индекс «в»).

В соответствии с этим объемные доли шаров и зерен выразятся несколько иначе:

(4)

(5)

как и константа скорости измельчения

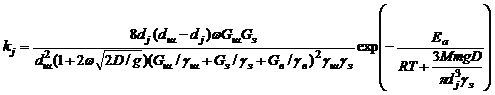. (6)

Интегральная формула (2) при этом остается без изменений. Вполне очевидно, что уточненная формула константы представляется более общей, так как она сводится к (1) при G _в =0, т. е. для сухого измельчения.

Формулы (6) и (2) были запрограммированы на языке Delphi 7 с вводом исходных данных на основе характеристик руды и мелющих шаров, а также параметров и режима работы мельницы.

Для проверки уточненной модели измельчения опыты проводили в лабораторной шаровой мельнице 62МЛ на забалансовой медно-сульфидной руде (Центральный Казахстан). Для проверки принципиальной применимости вероятностной модели (1, 2) использовали узкую фракцию -0,5+ 0,2 мм со средним размером d ₁ = 3,5·10 ^{- 4 м , общей массой G} _з = 0,200 кг , плотностью γ _з = 2650 кг/м ³ . Стальные шары размером d _ш =0,0221 м, массой m =0,0476 кг, плотностью γ _ш =7874 кг/м ³ и общей массой G _ш =1,470 кг загружали в мельницу вместе с водой массой G _в =0,350 кг и плотностью γ _в =1000 кг/м ³ . Внутренний диаметр мельницы составил D =0,1455 м, угловая скорость вращения ω для поддержания водопадного режима задавалась равной 1,87 с ^-1 .

Руда более чем на половину состоит из кварцита, поэтому за ее вещественную характеристику приняли кварц с =0,0601 кг/моль, а в качестве энергетического барьера активации – его теплоту плавления с учетом полиморфных превращений Е _а =9170 Дж/моль в соответствии с рекомендациями авторов теории [1–4]. При фракционном анализе продуктов измельчения использовали стандартный набор сит, в данном случае начиная с первой фракции -0,5+ 0,2 мм ( d ₁ = 3,5·10 ^-4 м), далее вторая фракция -0,2+ 0,1 мм ( d ₂ = 1,5·10 ^-4 м), третья -0,1+ 0,071 мм ( d ₃ = 8,55·10 ^-5 м), а четвертая – последняя, размером -0,071+ 0 мм . В отношении представления последней фракции средним размером для сопоставления с результатами расчета по модели (2) существуют определенные проблемы, так как по новой модели тонкие классы учитываются более детально в полном соответствии с действительным фракционным составом нижнего класса, измельчение которого подчинено общим закономерностям последовательного разрушения зерен примерно на 8 осколков, т.е. с уменьшением размера в среднем в два раза, вплоть до сколь угодно малого размера [5]

. (7)

Таким образом, набор фракций и констант скоростей формируется по трем ситовым и остальным расчетным, находимым по формуле (7). Опыты проводили в течение 60, 300 и 900 с. Результаты в сопоставлении с расчетными значениями приведены в табл. 1.

В целом по экспериментальному массиву данных коэффициент корреляции составил R =0,530 при его значимости t _R =2,30>2, что соответствует адекватности использованной модели с 95% уровнем ее достоверности. Особенно важно то, что эта адекватность достигнута за счет учета в константе скорости (6) содержания воды в смеси шаров и рудных зерен, так как без этого учета получается совершенно неадекватная картина процесса, вызванная существенным завышением константы скорости.

Таблица 1. Зависимость опытного и расчетного выхода фракций ( P _j,э и P _j,р )

от продолжительности (τ) измельчения забалансовой медносульфидной руды.

Указаны начальное содержание фракций ( P _0j ), средние размеры зерен ( d _j )

и константы скорости измельчения ( k _j )

j	d j, м	k j , c -1	Р oj	τ = 60 с		τ =300 с		τ =900 с
				P j,э	P j,р	P j,э	P j,р	P j,э	P j,р
1	3,500·10 -4	4,158·10 -3	1	0,652	0,780	0,238	0,288	0,008	0,024
2	1,500·10 -4	2,262·10 -3	0	0,199	0,206	0,407	0,483	0,262	0,235
3	8,550·10 -5	1,315·10 -3	0	0,012	0,015	0,041	0,198	0,110	0,427
4	4,275·10 -5	6,612·10 -4	0	-	0,000	-	0,030	-	0,267
5	2,138·10 -5	3,311·10 -4	0	-	0,000	-	0,001	-	0,045
6	1,069·10 -5	1,656·10 -4	0	-	0,000	-	0,000	-	0,003
7	5,344·10 -6	8,283·10 -5	0	-	0,000	-	0,000	-	0,000
	Выход фракции -7,1 ·10 -5		-	0,137	0,000	0,314	0,032	0,620	0,314
	Σ		1	1,000	1,001	1,000	1,000	1,000	1,001

Таким образом, п роведенная прямая проверка теоретической модели измельчения по данным переработки монофракции медносульфидной руды в лабораторной шаровой мельнице при водопадном режиме работы показала, что опытные и расчетные данные находятся в удовлетворительном согласии.

Список использованных источников:

1. Малышев В. П. Разработка теории соударений для измельчения материалов / В. П. Малышев // Компл. использ. минер. сырья. – 1992. – № 12. – С. 43–49.

2. Малышев В. П. Новый аспект в теории измельчения руд и управления этим процессом / В. П. Малышев // Обогащение руд. – 1995. – № 4–5 (240–241). – С. 4–14.

3. Малышев В. П. Развитие теории измельчения руд на основе молекулярных подходов / В. П. Малышев, А. М. Турдукожаева, Д. Кайкенов // Обогащение руд. – 2012. – № 4. – С. 29–35.

4. Малышев В. П. Самоорганизация процесса измельчения руд в шаровых мельницах как результат подобия с кинетикой последовательных химических реакций / В. П. Малышев // Автоматика-информатика. – 2012. – № 3–4. – С. 15–31.

5. Ходаков Г. С. Физика измельчения / Г. С. Ходаков. – М.: Наука, 1972. – 308 с.