Іванов В. І. * , к. т. н. Радченко Ю. М. ** , к. т. н. Нестеренко Т. М. * ,
к. т. н. Зінченко В. Ю. * , к. пед. н. Мосейко Ю. В. *
* Запорізька державна інженерна академія, Україна;
** Національна металургійна академія України, м. Дніпропетровськ
ФІЗИКО-МАТЕМАТИЧНА МОДЕЛЬ ДИФУЗІЙНОГО ПЕРЕНЕСЕННЯ ТЕПЛОВОЇ ЕНЕРГІЇ ТА МАСИ РЕЧОВИНИЗА ПЕРЕХРЕСНИХ ЕФЕКТІВ
На підставі положень термодинаміки необоротних процесів [1] рушійними силами процесів перенесення теплової енергії та маси речовини слугують відповідно
і
:
, (1)
, (2)
де
– різниця хімічних потенціалів перенесення двох компонентів маси.
Зазначені термодинамічні сили є векторами (тензорами першого рангу), тому згідно принципу Кюрі цілком припустимим є їх поєднання, тобто рушійна сила, що обумовлює потік теплової енергії, може спричинювати потік маси речовини та навпаки.
Таким чином, потоки теплової енергії та маси речовини за наявності перехресних ефектів визначаються відповідно співвідношеннями:
; (3)
, (4)
де
,
– кінетичні коефіцієнти перенесення теплової енергії на маси речовини відповідно.
На підставі принципу взаємності Онзагера можна записати таку рівність:
;
,
. (5)
Маючи на увазі, що для двокомпонентної системи потенціал перенесення маси описується співвідношенням [2]:
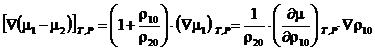, (6)
вводять позначення:
; (7)
;
(8)
;
(9)
та одержують:
; (10)
. (11)
Згідно із рівнянням Умова можна записати:
; (12)
. (13)
Враховуючи, що
, рівняння (12) переписують як
. (14)
Для зональних розрахунків, тобто за
і
рівняння (14) набуває вигляду:
, (15)
де
– коефіцієнт температуропровідності системи під час перенесення теплової енергії в ній за рахунок градієнта температури,
;
– коефіцієнт теплопровідності системи за наявності градієнта потенціалів перенесення маси (концентрації маси речовини
);
– коефіцієнт температуропровідності системи за дифузійного перенесення в ній
-го компонента,
.
Аналіз розмірності коефіцієнта
показує, що його можна подати у вигляді співвідношення:
, (16)
де
– коефіцієнт питомої масоємності системи за дифузійного перенесення теплової енергії масою речовини.
Таким чином, рівняння теплопровідності за наявності перенесення маси (15) можна записати як
. (17)
Аналогічно розглядають процес перенесення маси за перехресним ефектом.
Так, із рівняння (13) з урахуванням співвідношень (9) одержують
, (18)
де
– коефіцієнт масопровідності системи за наявності градієнта температур на ізопотенціальних поверхнях, тобто коефіцієнт термодифузії;
– коефіцієнт потенціалопровідності системи під час перенесення маси за рахунок градієнта потенціалів перенесення маси, тобто коефіцієнт дифузії.
Аналіз розмірності коефіцієнта потенціалопровідності
свідчить про сожливість його подавання через співвідношення
, (19)
де
– коефіцієнт масопровідності системи;
– коефіцієнт питомої масоємності системи за дифузійним перенесенням маси речовини.
Виділяють частину дифузійного потоку маси у рівнянні (11), що є наслідком наявності градієнта температур
. (20)
Такий потік може бути подано як
, (21)
де
– коефіцієнт питомої енергоємності системи на перенесення маси.
Тоді
(22)
чи з урахуванням того, що
, де
– коефіцієнт термодифузії, можна записати у вигляді:
. (23)
Таким чином, аналіз особливостей дифузійних процесів перенесення теплової енергії та маси речовини у системі, яку розглядають, з позицій феноменологічної термодинаміки дозволяє одержати систему диференційних рівнянь перенесення теплоти та маси за наявності перехресних ефектів у вигляді:
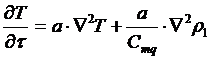; (24)
. (25)
Список використаних джерел:
1. Хаазе Р. Термодинамика необратимых процессов / Р. Хаазе ; под ред. А. В. Лыкова . – М.: Мир, 1967. – 644 с.
2. Лыков А. В. Тепломассообмен : справочник / А. В. Лыков . – М.: Энергия , 1972. – 554 с.