Докт. физ.-мат. наук Косолап А. И., Лисьих В. И.

Украинский государственный химико-технологический университет, Украина

ОПТИМАЛЬНОЕ РАЗМЕЩЕНИЕ КОМПОНЕНТОВ НА ИНТЕГРАЛЬНЫХ СХЕМАХ

В современных электронных устройствах самых различных сфер применения, начиная от бытовых приборов, компьютеров и заканчивая сложными научными электроприборами, сложно найти прибор, в котором бы не применялись интегральные схемы. Иногда одна микросхема выполняет практически все функции в электронном приборе. Микросхема объединяет в себе электронную схему, где все элементы (транзисторы, диоды, резисторы, конденсаторы) и электрические связи между ними конструктивно выполнены на одном кристалле. Поскольку размеры отдельных компонентов очень малы (микро- и нанометры), то на одном кристалле при современном развитии технологий, можно поместить более миллиона электронных компонентов. Наряду с поиском новых материалов для интегральных схем существует проблема оптимального размещения компонентов на ней.

Интегральную схему будем представлять в виде некоторой прямоугольной пластины, а компоненты, которые размещаются на ней – прямоугольниками. Компоненты связаны между собой. Эти связи можно представить графом G(N, V), вершины которого соответствуют компонентам, а дуги соединениям. Здесь N – множество вершин, равное количеству компонентов на схеме, а V – множество его дуг, равное количеству соединений между компонентами. Быстродействие интегральной схемы зависит от длины соединений, поэтому в качестве критерия расположения компонентов на схеме выберем суммарную длину соединений.

Обычно компонент схемы можно представить некоторым прямоугольником, который располагается на схеме таким образом, что его стороны параллельны сторонам схемы. Будем представлять прямоугольники в виде объединения квадратов c координатами (x_i, y_i). Тогда, если первый прямоугольник, например, состоит из четырех равных квадратов расположенных в линию, то должны выполняться следующие условия

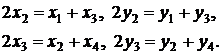
Если же эти четыре квадрата образуют новый квадрат, то это однозначно задается условиями

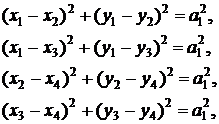
где a₁ – сторона каждого квадрата. Заметим, что для данного квадрата полученные квадратичные условия можно заменить линейными.

Одним из ограничений в математической модели оптимального расположения компонентов на схеме будет условие непересечения компонентов. Достаточным условием непересечения компонентов является следующая система квадратичных неравенств

где a_i – сторона i-го квадрата.

Каждый компонент схемы должен полностью располагаться на схеме. Это определяется следующими неравенствами

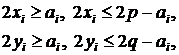
где (p, q) – стороны схемы.

Целевая функция для этой задачи запишем в виде

Часть приведенных ограничений будут избыточными. Это зависит от набора компонент.

В данной постановке решение задачи заключается в минимизации выпуклой квадратичной функции при общих квадратичных и линейных ограничениях. Такая задача является многоэкстремальной.

Рассмотрим частный случай этой задачи, когда прямоугольные компоненты можно представить линейной последовательностью квадратов. В этом случае, квадратичными ограничениями будут только условия непересечения компонентов. Запишем эти условия в виде

.

Используем точную квадратичную регуляризацию для преобразования данной задачи к виду

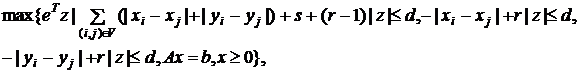(1)

где z = (x, y, z₁), |z| = |x₁|+…+|x_n|+|y₁|+…+|y_n|+|z₁|, параметр r > 0 выбирается таким, чтобы допустимое множество задачи (1) было выпуклое. Линейные условия Ax = b задают принадлежность квадратов компонентам. Значение параметра s удовлетворяет условию

где (x^*, y^*) – искомое решение задачи.

В задаче (1) необходимо найти минимальное значение d, при котором ее решение удовлетворяет условию r|z| = d с заданной точностью. Такое значение d находим методом дихотомии.

При фиксированном значении d задача (1) будет выпуклой, однако ее функции являются негладкими. Для решения задачи (1) при фиксированном значении d использовался метод последовательного раскрытия модулей [1]. Проведенные численные методы показали, что предлагаемый метод решения данного класса задач является эффективным.

Список использованных источников:

1. Косолап А. И. Методы глобальной оптимизации / А. И. Косолап. – Днепропетровск : Наука и образование, 2013. – 316 с.