Наши конференции
В данной секции Вы можете ознакомиться с материалами наших конференций
II МНПК "Спецпроект: анализ научных исследований"
II МНПК"Альянск наук: ученый ученому"
I Всеукраинская НПК"Образовательный процесс: взгляд изнутри"
II НПК"Социально-экономические реформы в контексте европейского выбора Украины"
III МНПК "Наука в информационном пространстве"
III МНПК "Спецпроект: анализ научных исследований"
I МНПК "Качество экономического развития"
III МНПК "Альянс наук: ученый- ученому"
IV МНПК "Социально-экономические реформы в контексте интеграционного выбора Украины"
I МНПК "Проблемы формирования новой экономики ХХI века"
IV МНПК "Наука в информационном пространстве"
II МНПК "Проблемы формирования новой экономики ХХI века"
I НПК "Язык и межкультурная коммуникация"
V МНПК "Наука в информационном пространстве"
II МНПК "Качество экономического развития"
IV МНПК "Спецпроект: анализ научных исследований"
ІІІ НПК "Образовательный процесс: взгляд изнутри"
VI МНПК "Социально-экономические реформы в контексте интеграционного выбора Украины"
МНПК «Проблемы формирования новой экономики ХХI века»
IV МНПК "Образовательный процесс: взгляд изнутри"
IV МНПК "Современные проблемы инновационного развития государства"
VI МНПК «Наука в информационном пространстве»
IV МНПК "Проблемы формирования новой экономики ХХI века"
II МНПК студентов, аспирантов и молодых ученых "ДЕНЬ НАУКИ"
VII МНРК "Социально-экономические реформы в контексте интеграционного выбора Украины"
VI МНПК "Спецпроект: анализ научных исследований"
VII МНПК "Наука в информационном пространстве"
II МНК "Теоретические и прикладные вопросы филологии"
VII МНПК "АЛЬЯНС НАУК: ученый - ученому"
IV МНПК "КАЧЕСТВО ЭКОНОМИЧЕСКОГО РАЗВИТИЯ: глобальные и локальные аспекты"
I МНПК «Финансовый механизм решения глобальных проблем: предотвращение экономических кризисов»
I Международная научно-практическая Интернет-конференция «Актуальные вопросы повышения конкурентоспособности государства, бизнеса и образования в современных экономических условиях»(Полтава, 14?15 февраля 2013г.)
I Международная научно-практическая конференция «Лингвокогнитология и языковые структуры» (Днепропетровск, 14-15 февраля 2013г.)
Региональная научно-методическая конференция для студентов, аспирантов, молодых учёных «Язык и мир: современные тенденции преподавания иностранных языков в высшей школе» (Днепродзержинск, 20-21 февраля 2013г.)
IV Международная научно-практическая конференция молодых ученых и студентов «Стратегия экономического развития стран в условиях глобализации» (Днепропетровск, 15-16 марта 2013г.)
VIII Международная научно-практическая Интернет-конференция «Альянс наук: ученый – ученому» (28–29 марта 2013г.)
Региональная студенческая научно-практическая конференция «Актуальные исследования в сфере социально-экономических, технических и естественных наук и новейших технологий» (Днепропетровск, 4?5 апреля 2013г.)
V Международная научно-практическая конференция «Проблемы и пути совершенствования экономического механизма предпринимательской деятельности» (Желтые Воды, 4?5 апреля 2013г.)
Всеукраинская научно-практическая конференция «Научно-методические подходы к преподаванию управленческих дисциплин в контексте требований рынка труда» (Днепропетровск, 11-12 апреля 2013г.)
VІ Всеукраинская научно-методическая конференция «Восточные славяне: история, язык, культура, перевод» (Днепродзержинск, 17-18 апреля 2013г.)
VIII Международная научно-практическая Интернет-конференция «Спецпроект: анализ научных исследований» (30–31 мая 2013г.)
Всеукраинская научно-практическая конференция «Актуальные проблемы преподавания иностранных языков для профессионального общения» (Днепропетровск, 7–8 июня 2013г.)
V Международная научно-практическая Интернет-конференция «Качество экономического развития: глобальные и локальные аспекты» (17–18 июня 2013г.)
IX Международная научно-практическая конференция «Наука в информационном пространстве» (10–11 октября 2013г.)
К . ф .- м . н . Непочатенко В . А ., к . ф .- м . н . Розумнюк В . Т ., к.ф.-м.н. Шевченко Р.Л., Непочатенко И.А.
Белоцерковский национальный аграрный университет
Предельная фазовая граница при фазовом переходе второго рода в сегнетоэластике BiVO 4
Сегнетоэластики являются хорошими модельными объектами при изучении структурных фазовых переходов, поскольку в этих кристаллах упругие взаимодействия при полиморфных фазовых переходах можно исследовать в “чистом” виде [1]. Для фазовых переходов первого рода предложена модель плоской бесструктурной тонкой фазовой границы (ТФГ) [2] и сделан анализ условий ее формирования для фаз с разной симметрией [3 ; 4]. ТФГ соответствует недеформированной плоскости (как правило, с иррациональными индексами) при наличии небольшого относительного поворота кристаллографических осей диссимметричной фазы относительно исходной фазы. Получены два уравнения ТФГ, которые формируют два близких (субориентационных) состояния. Субориентационные состояния отличаются знаком угла и направлением оси вращения относительно исходной фазы и принадлежат к различным типам структурных доменов [ 5 ] . В [ 5 ] показано, что ориентации фазовых границ и макропараметры, формируемой при фазовом переходе доменной структуры в Pb 3 ( PO 4 ) 2 , хорошо соответствуют модели ТФГ.
Доменная структура сегнетоэластика BiVO
4
формируется при фазовом переходе второго рода
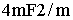 . Однако, количество возможных ориентационных состояний, существование субориентационных состояний в этом кристалле можно объяснить, применяя модель ТФГ, которая применяется при фазовых переходах первого рода. Поскольку при структурном фазовом переходе второго рода симметрия может изменяться только скачком [ 6 ] , то в данной работе предлагается рассматривать этот тип фазового перехода как предельный случай фазового перехода первого рода с бесконечно малыми изменениями кристаллографических параметров решетки, а следовательно, существованием предельной фазовой границы (ПФГ), разделяющей две фазы с разной симметрией.
. Однако, количество возможных ориентационных состояний, существование субориентационных состояний в этом кристалле можно объяснить, применяя модель ТФГ, которая применяется при фазовых переходах первого рода. Поскольку при структурном фазовом переходе второго рода симметрия может изменяться только скачком [ 6 ] , то в данной работе предлагается рассматривать этот тип фазового перехода как предельный случай фазового перехода первого рода с бесконечно малыми изменениями кристаллографических параметров решетки, а следовательно, существованием предельной фазовой границы (ПФГ), разделяющей две фазы с разной симметрией.
УРАВНЕНИЕ ПРЕДЕЛЬНОЙ ФАЗОВОЙ ГРАНИЦЫ
Предельная фазовая граница соответствует условиям формирования ТФГ [ 3 ] , поэтому ее ориентацию в кристалле можно получить из уравнений ТФГ, используя соответствующие предельные значения параметров решетки при фазовом переходе.
Согласно [3], уравнение тонкой поверхности раздела тетрагональной фазы, с кристаллографическими параметрами a
1
, c
1
, и моноклинной фазы, с параметрами a
2
, b
2
, c
2
, ?
2
=?
2
–90
0
, в СК первой фазы (ось
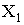 параллельна оси
параллельна оси
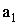 ,
,
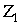 - оси
- оси
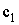 ) имеет вид:
) имеет вид:
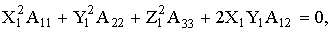 (1)
(1)
где
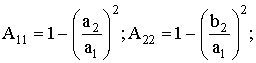
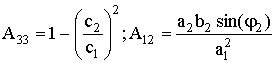 ,
,
Уравнение (1) при условии
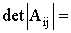
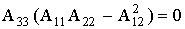 (2)
(2)
соответствует уравнению двух пересекающихся плоскостей. Возможны два варианта:
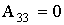 , (3)
, (3)
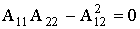 . (4)
. (4)
Уравнения ТФГ, полученные при выполнении условия (4), не соответствуют симметрии параэластической фазы. Если реализуется (3), то
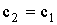 (параметр с при фазовом переходе не меняется) и (1) соответствует следующим уравнениям двух ТФГ
(параметр с при фазовом переходе не меняется) и (1) соответствует следующим уравнениям двух ТФГ
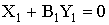 , (5)
, (5)
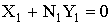 , (6)
, (6)
где
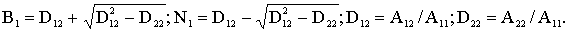
Уравнения этих ТФГ можно получить в СК сегнетоэластической фазы [ 3 ].
Из анализа температурной зависимости параметров решетки в BiVO
4
[ 7 ] нами получено, что наблюдаются линейные зависимости параметра
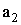 и
и
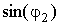 от величины
от величины
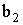 . Этим линейным зависимостям соответствуют следующие уравнения регрессий:
. Этим линейным зависимостям соответствуют следующие уравнения регрессий:
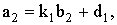 (7)
(7)
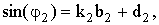 (8)
(8)
где
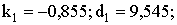
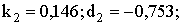
Поскольку в районе фазового перехода второго рода
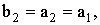
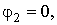 то из (7) определяем значение
то из (7) определяем значение
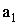
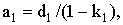 (9)
(9)
а из (8) получаем второе значение
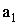 (обозначим его
(обозначим его
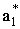 )
)
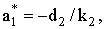 (10)
(10)
которое отличается от
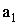 в четвертом знаке после запятой. Так как,
в четвертом знаке после запятой. Так как,
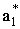 и
и
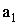 должны быть равными, то проведем коррекцию
должны быть равными, то проведем коррекцию
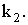 Из (10) получаем:
Из (10) получаем:
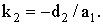 (11)
(11)
Подставляя в (5) и (6) полученные линейные зависимости параметров решетки (7), (8) с учетом поправки (11) и, переходя к предельному значению
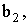 получаем уравнения двух ПФГ в СК
получаем уравнения двух ПФГ в СК
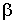 - фазы
- фазы
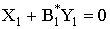 , (12)
, (12)
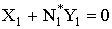 , (13)
, (13)
где
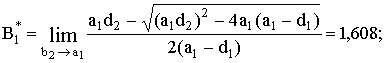
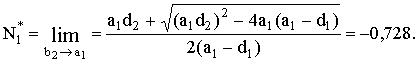
ПФГ (12), (13) формируют два субориентационных состояния, СК которых повернуты вокруг оси
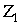
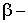 фазы, соответственно на бесконечно малые углы
фазы, соответственно на бесконечно малые углы
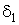 0 и
0 и
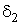 0. Применяя к фазовым границам операцию симметрии
0. Применяя к фазовым границам операцию симметрии
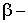 фазы (ось симметрии 4 порядка), получаем еще два уравнения ПФГ
фазы (ось симметрии 4 порядка), получаем еще два уравнения ПФГ
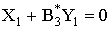 , (14)
, (14)
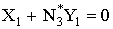 , (15)
, (15)
где
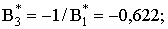
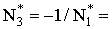 1,375,
1,375,
которые формируют еще два ориентационных состояния.
Таким образом, в BiVO 4 возможно образование 4 ориентационных состояний, что подтверждается экспериментальными данными [ 8; 9 ].
Литература:
1. Л .А. Шувалов. Изв. АН СССР. Сер. физ. 43 , 1554 (1979).
2. Е.Ф. Дудник, В.А. Непочатенко. Кристаллография. 25 , 984 (1980).
3. В.А. Непочатенко, И.А. Непочатенко. Укр . Физ . Журн . 50 , 64 (2005).
4. В . А . Непочатенко . Укр . Физ . Журн. 50 , 483 (2005).
5. В.А. Непочатенко , Кристаллография. 50 , 847(2005).
6. Б.К. Вайнштейн, В.М. Фридкин, В.Л. Инденбом. Современная кристаллография – М ., 1979. Т .2. - 360с.
7. W. I. F. David, I.G. Wood. J.Phys.C: Solid State Phys. 16, 5127 (1983).
8 L .S. Wainer, R.F. Baggio, H.L. Dussel, M.A.R. Benyacar. Ferroelectrics. 31 , 121(1981).
9. W. I. F. David, I.G. Wood. J.Phys.C: Solid State Phys. 16, 5149 (1983).