WEB-ресурс научно-практических конференций

К.т.н . Гребенюк С.Н., д.т.н . Гоменюк С.И.

Запорожский национальный университет

Расчет напряженно-деформированного состояния эластомерных элементов грохотов в условиях вязкоупругого деформирования

Основным направлением совершенствования современной техники грохочения является использование эластомерных элементов в качестве просевающих поверхностей [1]. Наряду с традиционными конструкциями резиновых сит, становится целесообразным применение резонирующих ленточно-струнных сит, которые лишены недостатков, присущих традиционным конструкциям резиновых сит.

Резонирующее ленточно-струнное сито представляет собой просевающую поверхность, состоящую из отдельных элементов – лент-струн с периодическими выступами-зубцами с одной стороны ленты (рис.1). Ленты-струны устанавливаются с относительным натяжением (25-30%) в специальных опорах подситника грохота.

Исследование напряженно-деформированного состояния таких конструкций связано с определенными трудностями, обусловленными как необходимостью учета некоторых отличительных свойств эластомеров, так и сложностью геометрической формы и условий работы конструкции.

Для описания вязкоупругих свойств материала при деформировании используются дифференциальные и интегральные соотношения. Наиболее общими и широко используемыми являются интегральные соотношения на основе наследственной теории Больцмана-Вольтерра . Для описания реологических характеристик эластомеров в интегральных соотношениях наиболее часто используются разностные ядра Ю.Н. Работнова , А.Р. Ржаницина и М.А. Колтунова . В работах В.Н. Потураева , В.И. Дырды и других [2; 3] представлен большой объем экспериментальных исследований процессов деформирования эластомерных конструкций, изучены вязкоупругие свойства резин. Также ядро Ю.Н. Работнова широко использовано для расчета конструкций из эластомеров в работах Э.Э. Лавендела и его сотрудников [4, 5]. Теоретические и экспериментальные исследования вязкоупругого поведения полимерных материалов проведены в работе [6]. Методика расчета эластомерных конструкций на основе метода конечных элементов с учетом вязкоупругих свой ств пр едложена в работах В.В. Киричевского и его учеников [7; 8]. В том числе был проведен расчет эластомерных элементов сит грохотов в упругой постановке в работе [9], и в упругой и вязкоупругой постановке для эластомерной ленты-струны с трещиной в статье [10].

Исследование напряженно-деформированного состояния таких конструкций связано с необходимостью учета некоторых отличительных свойств эластомеров, таких как слабая сжимаемость, реологический характер зависимости между усилиями и перемещениями. Учет всех этих свойств вызывает определенные математические трудности. Одним из наиболее эффективных численных методов расчета конструкций является метод конечных элементов. Для учета слабой сжимаемости материала воспользуемся моментной схемой конечного элемента [7].

Для учета вязкоупругих свойств материала воспользуемся наследственной теорией Больцмана-Вольтерра . Ввиду того, что вязкая составляющая энергии деформации является функцией времени и перемещений, задача вязкоупругости становится нелинейной. Для определения дополнительной нагрузки воспользуемся традиционным подходом построения уравнений МКЭ на основе вариации полной потенциальной энергии системы:

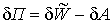. (1)

Здесь 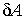– вариация работы распределенных объемных P ⁱ и поверхностных F ⁱ сил

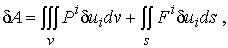(2)

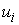– вектор перемещений, 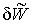– вариация внутренней энергии вязкоупругой деформации

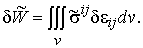(3)

Выражение для тензора упругих напряжений запишется в виде:

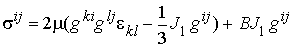, (4)

где 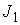– первый инвариант тензора деформаций, 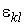– компоненты тензора деформаций, 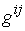– компоненты метрического тензора.

В предположении о релаксации сдвигового модуля 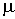и отсутствии релаксации объемного B , выражение (4) для вязкоупругого материала запишется в виде:

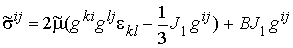, (5)

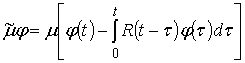где . (6)

Тогда соотношение (5) с учетом выражения (6) примет вид

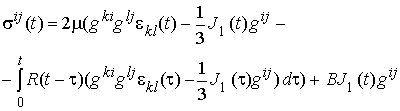. (7)

Для реализации решения методом конечных элементов, считая, что перемещения u ( t ) и деформации 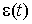изменяются линейно внутри каждого интервала времени, представим соотношение (7) в конечно-разностной форме

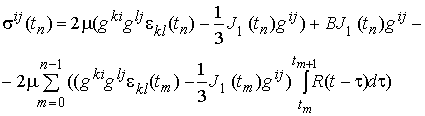. (8)

Учитывая, что линейная составляющая шаровой части тензора напряжений равна

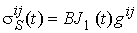, (9)

линейная составляющая девиаторной части тензора напряжений равна

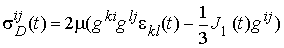, (11)

выражение (8) запишется в виде:

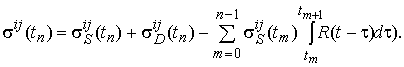(13)

Подставим компоненты тензора напряжений (13) в вариацию энергии деформации (1), тогда получим:

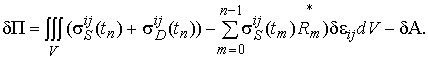(14)

Здесь .

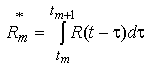Выделим линейные составляющие вариации энергии упругой деформации, которые зависит от истории нагружения , но не зависит от закона изменения деформации во времени. Эти составляющие служат основой формирования матрицы жесткости для фиксированного момента времени t . Из выражения (14) можно записать, что

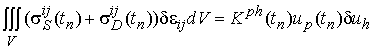. (15)

Наследственная часть матрицы жесткости запишется в виде:

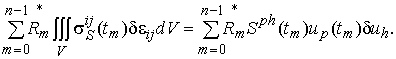(16)

Предполагая, что на тело действует только распределенная поверхностная нагрузка, которую можно свести к сосредоточенным узловым силам, и, принимая во внимание соотношения (15) и (16), вариация потенциальной энергии приобретет вид:

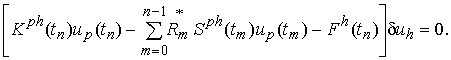(17)

Поскольку вариация перемещений не равна нулю, то нулю должно быть равно выражение в прямоугольных скобках, представляющее собой систему линеаризованных разрешающих уравнений наследственной вязкоупругости :

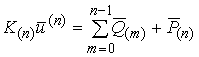(18)

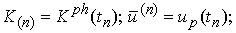
где 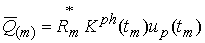– вектор дополнительной нагрузки; 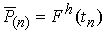– вектор распределенных поверхностных нагрузок, действующих на момент времени .

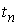Данная методика реализована в программном комплексе «МІРЕЛА+» [8], с помощью которого проведен расчет эластомерных элементов сит грохотов.

Исходные данные: длина 382 мм , ширина 13 мм , высота 26 мм , марка резины – 2959. Реологические параметры ядра Ю.Н. Работнова для данной марки резины: a = -0,6; b = 1,062; g = 0,64. Модуль сдвига G ₀ = 1760000 Па, n = 0,49. Предварительно лента-струна растягивалась в продольном направлении на 30 % от длины, а затем прикладывалась поверхностная нагрузка интенсивностью 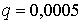МПа, моделирующая вес просеваемого материала. Сетка разбиения – 5?4?162.

Из анализа полученных результатов, некоторые из них представлены на рисунках 2 и 3 можно сделать следующие выводы:

-использование моментной схемы конечных элементов позволяет получить более достоверный результат при расчете слабосжимаемых конструкций по сравнению с традиционным МКЭ за счет учета эффекта «ложного сдвига»;

-максимальный прогиб в упругом случае на 20 % меньше максимального прогиба, полученного с учетом вязкоупругих свойств материала;

-нормальные напряжения в вязкоупругом случае на 6-14% меньше напряжений, полученных в упругом случае.

Рис.2. Перемещения ленты-струна в направлении толщины в случае упругого деформирования

Рис.3. Перемещения ленты-струна в направлении толщины в случае вязкоупругого деформирования

Литература:

1. Вайсберг Л.А. Проектирование и расчет вибрационных грохотов. – М.: Недра, 1986. – 144 с .

2. Потураев В.Н., Дырда В.И., Круш И.И. Прикладная механика резины. – К.: Наукова думка, 1980. – 260 с .

3. Дырда В.И. Прочность и разрушение эластомерных конструкций в экстремальных условиях. – К.: Наукова думка, 1988. – 232 с .

4. Лавендел Э.Э. Методы и алгоритмы решения прикладных задач связанной теории вязкоупругости для высокоэластичного материала (резины) / Механика эластомеров. – 1977. – Т. 1. – С. 65-74.

5. Дымников С.И., Лавендел Э.Э., Павловскис А.А., Сниегс М.И. Прикладные методы расчета изделий из высокоэластичных материалов. – Рига: Зинатне , 1980. – 238 с.

6. Каминский А.А., Гаврилов Д.А. Механика разрушения полимеров. – К.: Наукова думка, 1988. – 221 с .

7. Киричевский В.В. Метод конечных элементов в механике эластомеров. – К.: Наукова думка. 2002. – 655 с .

8. Метод конечных элементов в вычислительном комплексе МІРЕЛА+/ Киричевский В.В., Дохняк Б.М., Козуб Ю.Г. и др. – К.: Наукова думка, 2004. – 300 с .

9. Киричевський В.В., Гребенюк С.М., Гоменюк С.І., Киричевський Р.В. Чисельне моделювання напружено-деформованого стану еластомерних елементі в сит грохотів у САПР “МІРЕЛА+” // Радіоелектроніка . Інформатика . Управління . – Запоріжжя : ЗНТУ, 2005. – №2(14). – С.53-57.

10. Гребенюк С.Н., Дохняк Б.М., Киричевский Р.В., Киричевский В.В. Термомеханические параметры разрушения вязкоупругих элементов сит грохотов// В існик Східноукраїнського державного університету . – 1999. – №3(18). – С. 76-81.