WEB-ресурс научно-практических конференций

Антипова А.С., к.ф.-м.н . Бирюков В.Г.

Саратовский государственный университет им. Н.Г. Чернышевского, Российская Федерация

КИНЕМАТИЧЕСКАЯ ЗАДАЧА ПРОСТРАНСТВЕННОГО ОПТИМАЛЬНОГО РАЗВОРОТА ТВЁРДОГО ТЕЛА

Теория оптимального управления изучает методы решения задач о выборе наилучшего в некотором заранее определенном смысле способе осуществления управления некоторым динамическим процессом. В качестве критерия оптимальности может ставиться цель достижения максимума или минимума заданной совокупности критериев качества систем. Так, например, в рассматриваемой задаче ориентации в качестве критерия оптимальности выбирается минимизация интегрального квадратичного функционала качества, подынтегральной функцией которого являются компоненты вектора абсолютной угловой скорости. Такой функционал качества характеризует энергетические затраты на управление. Работа посвящена аналитическому и численному решению кинематической задачи оптимальной переориентации твёрдого тела, когда в качестве управляющего воздействия рассматривается вектор абсолютной угловой скорости тела. Эта задача имеет большое значение в механике космического полета и в задачах управления ориентации подвижных объектов.

Угловое движение твёрдого тела описывается кватернионным дифференциальным кинематическим уравнением:

,                                                   (1)

где   - кватернион, характеризующий ориентацию твёрдого тела относительно инерциальной системы координат,   - абсолютная угловая скорость твёрдого тела, заданная своими проекциями на оси связанной системы координат, знак « » означает кватернионное произведение, а точка означает дифференцирование по времени [1].

Рассмотрим кинематическую задачу оптимального управления угловым движением твердого тела. Задача заключается в построении оптимального управления (в качестве управления в кинематических задачах выступает вектор абсолютной угловой скорости ),   переводящего твёрдое тело из заданного начального углового положения, задаваемого кватернионом начальной ориентации

                                                      (2)

в заданное конечное угловое положение, задаваемое кватернионом конечной ориентации

                                                     (3)

при этом должен минимизироваться функционал качества

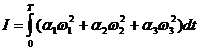,                                     (4)

где   (i=1,2,3) – проекции вектора на оси связанной с телом системы координат, - весовые множители функционала .

Функционал (4) характеризует, в некотором смысле, общие энергетические затраты на управление. Управление полагаем неограниченным, а время ориентации T – фиксированным (заданным).

Поставленная задача решалась применением метода Л.С. Понтрягина [3]. Следуя этому методу, была составлена функция Гамильтона-Понтрягина [4] и система однородных дифференциальных уравнений относительно сопряженных переменных

или в скалярном виде

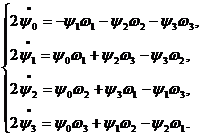                                      (5)

Для неограниченного управления из условия максимума функции Гамильтона–Понтрягина был получен закон оптимального управления как функция сопряженных переменных и весовых множителей функционала

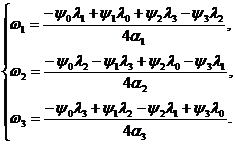                                (6)

В результате задача была сведена к решению системы дифференциальных уравнений (1) и (5), замкнутой относительно закона оптимального управления (6), с начальными условиями (2), (3).

После ряда преобразований, получаем систему дифференциальных уравнений для нахождения закона оптимального управления [2]

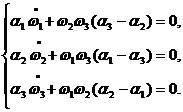                                        (7)

В частном случае равенства всех весовых множителей ( ) система, очевидно, имеет решение

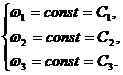                                                   (8)

Используя заданные начальные и конечные условия, получим, что оптимальное управление имеет вид

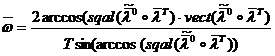.                               (9)

Этот случай соответствует плоскому развороту твёрдого тела.

При двух равных между собой весовых множителях   система (7) принимает вид

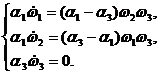                                             (10)

Решение этой системы запишется в виде

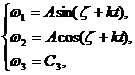                                                  (11)

где   постоянные интегрирования, определяемые из краевых условий.

Решения кватернионного дифференциального уравнения (1), замкнутого оптимальным управлением (11), имеет вид

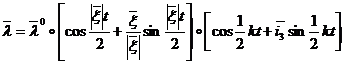,                 (12)

где   - постоянный вектор, который выражается через постоянные интегрирования   следующим образом . Для определения постоянного вектора   воспользуемся конечным условием (3)

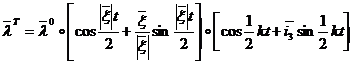                (13)

Введя , можем переписать (13) в скалярном виде

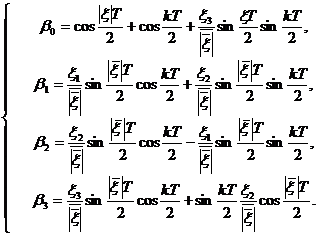                       (14)

Таким образом, для нахождения кватерниона ориентации твёрдого тела   остаётся найти компоненты . Они находятся численно, решая уравнение (14) относительно . Получив эти величины, можно найти раннее введённые , а после, пользуясь формулой (11), получить оптимальное управление   на каждом временном шаге .

Для численного решения системы (14) была разработана программа на языке программирования C#, реализующая метод Ньютона для нахождения неизвестного вектора   [5] . В качестве начального приближения для   выбирались компоненты вектора оптимального управления из (8). На рис.1, рис.2 представлены результаты численного решения задачи для выбранных граничных условий.

На рис.1 приведён график зависимости компонент кватерниона   ориентации   от времени при весовых множителях и времени переориентации T =30c.

Граничные условия задавались следующим образом:

начальное положение определялось кватернионом начальной ориентации

что соответствует самолётным углам ,

а конечное положение определялось кватернионом конечной ориентации

что соответствует самолётным углам .

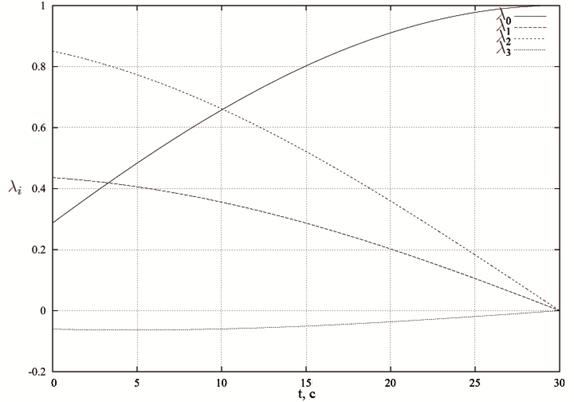
Рис. 1. Зависимость компонент кватерниона ориентации   от времени t для случая, когда

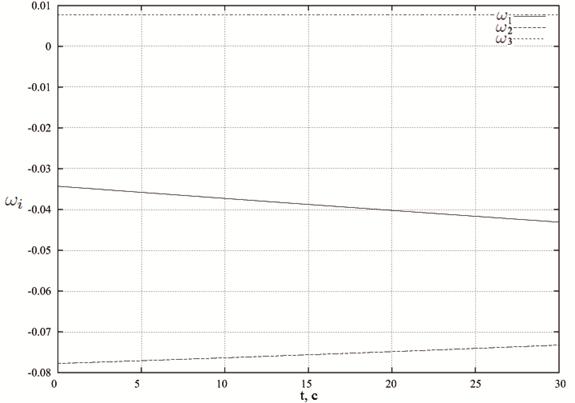
Рис. 2. График зависимости компонент вектора абсолютной угловой скорости   от времени t для случая

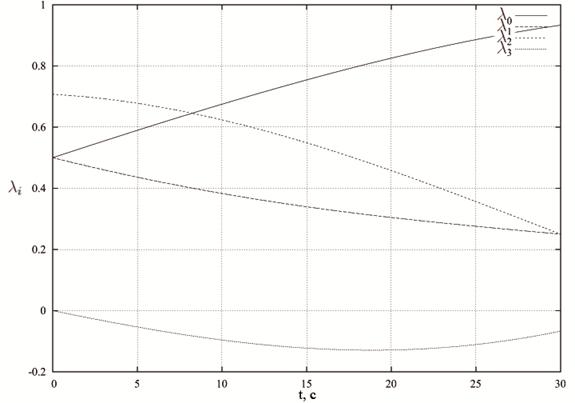
Рис. 3. Зависимость компонент кватерниона   ориентации   от времени t для случая, когда

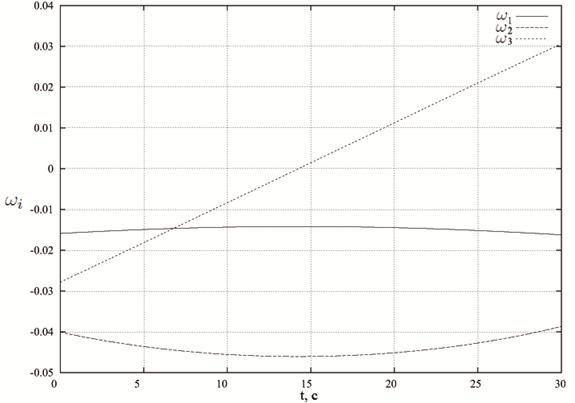
Рис. 4. График зависимости компонент вектора абсолютной угловой скорости   от времени t для случая

На рис.2 приведен соответствующий график компонент вектора абсолютной угловой скорости   от времени.

Рассмотренный случай называют регулярной прецессией.

Для самого общего случая уравнения (7), когда все весовые множители различны, то есть , решение задачи выражается в эллиптических функциях. Для решения задачи было построено численное решение на языке программирования C# [7]. На рис.3, рис.4 представлены результаты численного решения данной задачи для выбранных граничных условий.

На рис.3 представлен график зависимости компонент кватерниона   ориентации   от времени. Время переориентации задаётся равным T =30с, весовые множители .

Граничные условия:

начальное положение задавалось кватернионом начальной ориентации

а конечное положение задавалось кватернионом конечной ориентации

что соответствует в начальном положении самолётным углам , а в конечном положении самолётным углам .

На рис.4 приведен соответствующий график компонент вектора абсолютной угловой скорости   от времени.

Из приведенных рисунков видно, что построенные законы оптимального управления обеспечивают перевод тела из заданных начальных положений в заданные конечные положения.

Список использованной литературы:

1. Бранец В. Применение кватернионов в задачах ориентации твердого тела /В. Бранец , И. Шмыглевский . – М.: Наука, 1973. – 320 с .

2. Бухгольц Н. Основной курс теоретической механики. Ч. 2 / Н. Бухгольц . – М.: Наука, 1966. – 332 с .

3. Понтрягин Л.С. Математическая теория оптимальных процессов / [Л. С. Понтрягин, Е. Ф. Мищенко, В. Г. Болтянский , Р. В. Гамкрелидзе]. – М.: Наука, 1983. – 392 с .

4. Ройтенберг Я. Автоматическое управление / Я. Ройтенберг. – М.: Наука, 1971. – 396 с .

5. Гулин А. Численные методы / А. Гулин , А. Самарский . – М.: Наука, 1989. – 432 с .

6. Челноков Ю. Кватернионные и бикватернионные модели и методы механики твердого тела и их приложения. Геометрия движения / Ю. Челноков. – Саратов: СГУ им. Н. Г. Чернышевского, 2006. – 236 с .

7. Моисеев Н.   Численные методы в теории оптимальных систем/ Н. Моисеев. – М.: Наука, 1971. – 424 с .