WEB-ресурс научно-практических конференций

МОДЕЛИРОВАНИЕ ПРОЦЕССА ФОРМИРОВАНИЯ ЗНАНИЙ ДЛЯ ЦЕЛЕЙ УПРАВЛЕНИЯ УЧЕБНЫМ ПРОЦЕССОМ

А. А. Демин, С. И. Резников

Быстрое увеличение числа обучающихся, стремительный рост научных знаний в самых различных областях и, в первую очередь, в области информационных технологий, обусловливают потребность в разработке теории управления учебным процессом, одним из важнейших элементов которой являются математические модели формирования знаний и мониторинга качества обучения [1, 2, 3].

Представляется необходимой разработка модели формирования знания, которая позволяла бы прогнозировать состояние усвоения изучаемого материала обучаемыми. Допустим, что в результате изучения дисциплины обучаемый должен освоить N положений учебного материала. Под текущим L -м   состоянием обучаемого   будем понимать событие, когда обучаемый не знает L положений учебной дисциплины. Совокупность состояний   образует, таким образом, пространство состояний обучаемого , причем .

Пусть имеется некоторая справочная система, использование которой позволяет обучаемому переходить из состояния   в   и т.д., в то время как при забывании осуществляется переход в обратном направлении   и т.д. Будем рассматривать справочную систему как систему с обслуживанием заявок по усвоению (восстановлению) знаний. Будем также считать, что для хранения информации о содержании N положений учебной программы используется   N   элементов памяти. Каждое L -е положение характеризуется   средним временем забывания . Принято считать, что время забывания – непрерывная случайная величина с функцией распределения

,

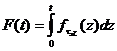где   - плотность распределения вероятности времени забывания L -го положения.

Примем закон распределения времени забывания экспоненциальным

,

где   - интенсивность забывания L -го положения.

Подобное допущение можно сделать по следующим соображениям:

-      в некоторых случаях действительно имеет место экспоненциальное распределение;

-      если эти распределения не являются экспоненциальными, то аппроксимация их экспоненциальными распределениями позволяет получить практически приемлемые инженерные оценки;

-      если поток учебного материала является простейшим, то характеристики динамики знаний в значительной степени определяются лишь средним временем восстановления, а не видом функции распределения [4];

-      асимптотические распределения, как показано в работе [4], часто являются экспоненциальными.

В результате принятой посылки получим плотность распределения времени забывания

.

Можно получить среднее значение времени забывания

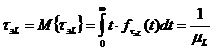
и оценку дисперсии времени забывания L - го положения для экспоненциального закона распределения .

Известно, что результирующие потоки заявок в системе обслуживания в большинстве случаев сходятся асимптотически к простейшему потоку, поэтому   будем считать, что поток заявок для восстановления знаний (поток забывания) является простейшим   пуассоновским потоком. Тогда вероятность появления k заявок в справочной системе на восстановление знаний в интервале времени [ 0, t ] определяется как

.

Примем, что распределение времени усвоения (восстановления) знаний также подчиняется экспоненциальному закону. Можно показать, что математическое ожидание времени усвоения (восстановления) знаний

,

где - интенсивность усвоения (восстановления) знаний.

Забывание положений учебной программы осуществляется параллельно, а восстановление - последовательно, т.е.

.

Если изучаемые положения однородны, то . На самом деле интенсивность забывания не является постоянной величиной для всех положений учебной программы. Проведенные исследования показали, что время забывания хорошо описывается авторегрессионной функцией второго порядка

.

С точки зрения теории массового обслуживания процесс формирования знаний представляет собой обслуживание простейшего пуассоновского потока заявок с экспоненциальным законом распределения длительности обслуживания (очереди ограниченной длины). Процесс изменения   знаний   можно описать как марковский случайный процесс с непрерывным временем. Было показано, на основании эргодической теоремы Маркова [5], что вероятности состояния системы обслуживания стремятся к предельным значениям. Поэтому стационарное распределение вероятностей системы может выступать как оценка текущего распределения. Предельную вероятность L -го состояния обучаемого тогда можно определить по формуле Эрланга [6]

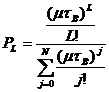  при .

Получение оценок состояния обучаемого на основе тестовых систем и сопоставление их с полученными вероятностными характеристиками позволяет формировать управленческие решения.

Рассмотренная модель формирования знаний ограничена рамками одной изучаемой дисциплины, тогда как   на практике приходится планировать и оптимизировать одновременное изучение нескольких дисциплин. Формализация таких процессов требует использования укрупненных агрегированных моделей.

Обозначим текущий уровень знаний обучаемого как . Модели динамики изменения знания Халла и Мастеллера-Буша описываются функцией вида

.

Такая функция является решением определенного дифференциального уравнения

.

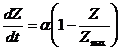Изменим данное уравнение так, чтобы оно учитывало процессы забывания информации и дискретный характер учебного материала. В результате получим

,

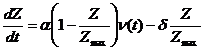где  

Параметр   является характеристикой способности усваивать информацию обучаемым, а параметр   характеризует интенсивность забывания информации. Решение для оценки уровня подготовки в - й день имеет вид

,

где - длительность занятий в - й учебный день.

В полученном решении учтена потеря работоспособности обучаемых , которая, общем случае, может быть описана функцией вида

.

В случае совместного изучения нескольких предметов можно записать систему уравнений для общей динамики знаний ,

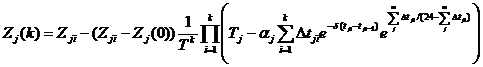где   - количество предметов;

  - уровень подготовки по - ому предмету в -й день;

  - требуемый уровень подготовки; - плановое время для изучения - ой дисциплины;

  - продолжительность занятий по - ому предмету в - ый день;

- коэффициенты усвоения и забывания информации.

Записанная система уравнений позволяет приступить к решению оптимизационной задачи распределения времени между изучаемыми дисциплинами. Представляется важным отметить тот факт, что рассмотренные в данной работе модели являются непротиворечивыми, хотя служат для формализации процессов приобретения знаний на разных иерархических уровнях.

Литература:

1. Свиридов А.П. Основы статистической теории обучения и контроля знаний. – М.: Высшая школа, 1981. - 272 с .

2. Методологические основы и математические методы /П од ред. Дж. Моудера , С.Элмаграби . – М.: Мир, 1981. - 712с.

3. Приобретение знаний /П од ред. Осуги С., Саэки Ю. -   М.: Мир, 1990. – 303 с.

4. Свиридов А.П. Введение в статистическую теорию обучения и контроля знаний. Ч.2. Элементы статистической динамики знаний. – М.: Высшая школа, 1974. - 189 с .

5. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. – М.: Наука, 1987. – 336 с .

6. Хинчин А.Я. Работы по математической теории массового обслуживания. – М.: Физматгиз , 1963. – 235 с.