ОТ НЕРАВЕНСТВ К ПОИСКУ ПРООБРАЗА ДАННОГО ОБРАЗА

Филер З. Ю.

( докт.тех.наук, канд. физ.-мат.наук, Кировоградский государственный педагогический университет, г. Кировоград, Украина)

Предложен метод невязки – введения параметра t >0, сводящий неравенство к уравнению. Множество решений х ( t ) этого уравнения является решением неравенства. Для квадратного неравенства с коэффициентами в R обнаруживаются и комплексные решения. Понятие неравенства обобщается как уравнение f ( x )= t y ⁰ , где y ⁰ – орт вектора в пространстве возможных значений функции. Это делает процесс решения неравенств частным случаем поиска прообраза данного образа.

1. Уравнение f ( x )=0. Задача о поиске корня функции – значения аргумента, обращающего её в 0, возникла ещё   в математике древних. Линейные и квадратные уравнения умели решать ещё в древности. Для иррациональных корней научились отыскивать высокоточные   приближения. В 1530–е годы, решая кубические уравнения, пришли к необходимости оперировать с квадратными корнями из отрицательных чисел. Идя по этому же пути, в 16-ом столетии научились решать с помощью радикалов и уравнения 4-ой степени. Дальнейшие попытки не приводили к цели до 1830-х годов, когда была доказана невозможность выражения корней с помощью радикалов для уравнений степени выше 4-ой. Но на грани 18 и 19 стол. К.Ф. Гауссом была доказана основная теорема алгебры о существовании комплексных корней уравнения любой степени с комплексными коэффициентами. В школе решают и простейшие показательные, логарифмические и тригонометрические уравнения, сводящиеся к линейным и квадратным

2. Неравенства f ( x ) < 0 ( f ( x ) > 0) с действительной функцией f ( x ) действительного аргумента х для многочленов первой степени решают, начиная   ещё с начальных классов. Однако, для многочленов 2-ой степени в случае отрицательного дискриминанта действительных решений может и не быть, а о существовании комплексных решений неравенств не подозревают и многие преподаватели не только средней школы, зная об отсутствии линейной упорядоченности во множестве комплексных чисел. Между тем, рассматривая процесс решения неравенства как поиск значений аргумента, удовлетворяющих неравенству ( поточечно ), мы легко сводим задачу к решению уравнения с параметром t – невязкой (разностью между левой и правой частями неравенства): f ( x ) + t = 0   ( f ( x ) = t ), t > 0 . Корни этого уравнения x ( t ) и дают нам множество Х – решение соответствующего неравенства, структурированное значениями невязки. Среди значений x ( t ) могут быть и комплексные числа. Для немонотонной функции f ( x ) множество Х структуризуется и частично упорядочивается значениями t .

2.1. Примеры. Неравенство х ² +4х+3 < 0 с помощью невязки t > 0 даёт уравнение х ² +4х+3+ t =0, корни которого х = -2 ± при t ? 1 действительны и образуют множество-интервал   Х ₀ = (-3;-1), получаемое любым классическим методом решения неравенств (интервалов, в том числе). При t > 1 получаем множество Х ₁ комплексных решений Х ₁ = { -2 ± і ? t > 1 } . Если Х ₀ есть отрезок действительной оси, то Х ₁ – прямая Reх=-2 , параллельная мнимой оси. Аналогично, неравенство х ² +4х+5 < 0 , не имеющее действительных решений, имеет комплексное решение - множество Х =        { -2 ± і ? t > 0 } .   Его точки расположены на той же прямой, но на расстоянии, большем 1 от действительной оси.

      Метод невязки даёт возможность проверки найденного решения. Как обычно, подставляя в уравнение, полученное вместо неравенства, найденное его решение х ( t ), мы должны получить равенство при всех значениях t , а при t > 0 - необходимый знак функции f ( x ). Так, для неравенства х ² +4х+5 < 0, эквивалентного уравнению х ² +4х+5 + t = 0 при t > 0 , мы получали х ( t ) =             -2 ± і ; подставив вместо х ( t ) его значение в левую часть неравенства, получим (– t ) и неравенство выполняется при всех положительных t .

2.2. Можно рассматривать и неравенство с комплекснозначными функциями. Например, «неравенство» ( 3+2і ) х < 7-і эквивалентно уравнению ( 3+2і ) х=7-і - t при t > 0 и имеет решение х ( t ) = ( 7-і – t )/ ( 3+2і )=((19-3 t ) - і (17-     -2 t ))/13. Оно описывает луч , исходящий из точки (19-17 і )/13 и проходящий через точку 1- і при t = 2. Понимая отсутствие линейного упорядочения во множестве комплексных чисел, данное неравенство можно принимать как равенство мнимых частей слева и справа и соответствующее неравенство действительных частей. Возможно отыскание комплексного х в виде х ₁ + іх ₂ с действительными х ₁ и   х _{2 ,} что приводит к системе, состоящей   из одного неравенства с 2 переменными и аналогичного уравнения. Описанный луч-решение является полупрямой, лежащей в соответствующей полуплоскости. Приведенное здесь его аналитическое отыскание в комплексном виде проще, чем решение описанной системы с 2 переменными.

2.3. Используя “основную теорему алгебры” (Даламбера – Гаусса), можно утверждать справедливость “основной теоремы алгебры многочленных неравенств”: Неравенство для многочленов с комплексными коэффициентами имеет   хотя бы комплексные решения” .

Отказ от привычных стереотипов “отрицательные числа логарифмов не имеют”, “квадратный корень из отрицательного числа не существует”, “синус не может быть больше 1 по модулю” и т.п. необходим. Замена этих фраз на “отрицательные числа действительных логарифмов не имеют”, “квадратный корень из отрицательного числа не существует во множестве действительных чисел” , “синус не может быть больше 1 по модулю для действительного аргумента” с показом существования соответствующих объектов во множестве комплексных чисел разрушают сложившиеся ложные стереотипы. Известен анекдот про студента, призванного в армию, где не очень грамотный ефрейтор рассказывает новобранцам о чём-то, что по мнению экс - студента противоречит науке: “Это не так, товарищ ефрейтор, ибо синус не может быть больше 1” . Ефрейтор строго замечает, что в боевой обстановке может! И ефрейтор прав, не зная даже ничего о существовании комплексных чисел. Используя формулу Эйлера, неравенство sina >1   сводим к неравенству с комплексными переменными ( е ^іа – е ^-іа )/ ( 2 і ) > 1 , откуда для аргумента синуса – числа а получаем уравнение с параметром у ² – 2іу ( 1+t ) – 1 = 0, у= е ^іа . Найдя у( t ), отыщем число а с помощью логарифмирования, используя формулу Lnz=ln|z| + i ( argz + 2k p ) , k ? Z . Для положительных t существует счётное   множество комплексных решений этого уравнения (рис. 1).

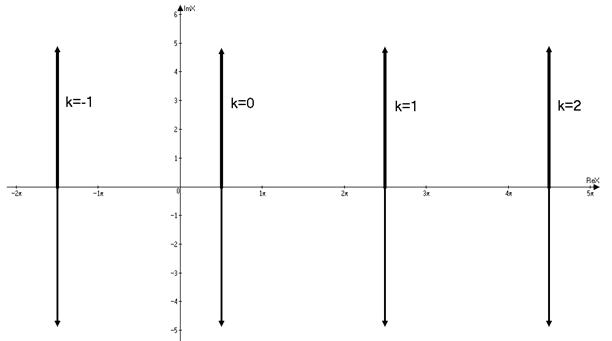
Рис. Решение неравенства sina >1

       Традиционные для введения в анализ упражнения на «отыскание области существования функции» (правильнее было бы сказать: аналитического выражения в области действительных чисел), как правило, сводятся к решению соответствующих неравенств. Допустив к рассмотрению и комплексный аргумент, в качестве ограничения будем иметь такие естественные факты, как невозможность деления на нуль , невозможность обращения   показательной функции в нуль, ибо е ^a+ib =e ^a e ^ib , | e ^ib |=1 , e ^a >0 при а, в ? R.

3. Двойное неравенство   А < f ( x ) < В сводится к уравнению f ( x ) = А+t (В-А), 0 < t < 1 . Неравенства типа | f ( x ) - А | < e , широко используемые в теории пределов, сводятся к уравнению f ( x ) = А- e + t *2 e и неравенству 0 < t < 1 . Для действительных значений х требуется по заданному e > 0 отыскать два положительных числа d ₁ и d ₂ , которые дадут интервал (окрестность) U = ( х ₀ - d ₁ , х ₀ + d ₂ ), для всех х из которого, образ f ( x ) будет находиться в e - окрестности числа А (предела функции при х ® х ₀ ). Окрестность U может быть выколотой, т.е. без точки х ₀ . Погоня за симметричной d - окрестностью точки х ₀ не является для действительных х необходимой. Для комплексных значений х и для векторов понятие   d - окрестности удобно, позволяя ограничивать область окружностью (сферой) радиуса d .

4. Обобщение понятия неравенства в комплексной области. Учитывая формулу Эйлера e ^{i j} = cos j + isin j ,   м ожно записать для уравнений

f ( x ) + t = 0   ( f ( x ) = t ), t > 0 , эквивалентных классическим неравенствам f ( x ) < 0 ( f ( x ) > 0), единую форму f ( x ) = t * e ^{i j} , где j = p в первом случае и j = 0 во втором. При других значениях   j мы получаем обобщение понятия неравенства как задачи поиска прообраза Х луча t * e ^{i j} для всех t > 0 при заданном угле j наклона к действительной   оси плоскости комплексного переменного образа f ( x ). Для отрезка луча А+ t (В-А) прообраз Х может быть найден с помощью обратной функции f ^–1 ( А+ t (В-А)) для t ? ( 0 ; 1 ) . Здесь А и В могут быть и комплексными числами.

4.1.   Для действительной функции действительного аргумента, не являющейся многочленом, отыскание комплексных корней представляет серьёзную проблему. Именно её приходится решать при каждом конкретном t . Тут можно рекомендовать численные методы типа «касательных» Ньютона, используя для поиска начального приближения к корню х ₀ точку положительного минимума (отрицательного максимума) для дифференцируемой функции, в которой производная равна нулю, а знак второй производной совпадает со знаком самой функции. Используя многочлен Тейлора второй степени в окрестности точки указанного экстремума f ( x ₀ ) + f ? ? ( x ₀ ) / 2 ( x-x ₀ ) ² , получим искомое комплексное начальное приближение х _{н =} х ₀ ± i . Затем можно уточнить корень и итерациями Ньютона; при этом важно, что f ? ( x _н ) ? 0 .

5. Описанные подходы могут быть использованы и для любого линейного нормированного пространства , в котором задаются значения функции f ( x ). Решение неравенства заменяется поиском прообраза для образа – луча t * у ⁰ , где у ⁰ – орт заданного направления в пространстве значений функции. Двойное неравенство заменяется отрезком «прямой» у ? { А+t (В-А) ? t ? ( 0 ; 1 ) } . Для односвязной области D в пространстве Y можно взять систему лучей, проходящих через граничную поверхность и выбранную внутреннюю точку.

6. Структуризация образа Y соответствующими значениями параметра t и направления у ⁰ образа у = t * у ⁰ вместе с алгоритмом решения уравнения f ( x )= t * у ⁰ позволяет использовать для поиска прообраза (а, следовательно, и для решения неравенств) компьютер. Каждой точке у образа ставится в соответствие некоторое множество точек прообраза Х ( t * у ⁰ ). Сетке в области Y отвечает некоторая сетка в области Х с «метками» t и у ⁰ . Для с епарабельных пространств это облегчает построение прообраза Х образа   Y .

Для функции f ( x , у) двух переменных х и у при каждом t _к получаем подмножество Х( t _к ) – линию уровня f ( x , у)= t _к и – «элементарное» решение неравенства f ( x , у) > 0 множество точек, где f ( x , у) = t _к > 0 . Для неравенства   f ( x , у, z ) > 0 элементарные подмножества Х( t _к ) являются поверхностями уровня   f ( x , у,z ) = t _к > 0 .

Выводы

1. Предложенный метод невязки позволяет находить и комплексные решения неравенств, в частности, квадратных, а также вводит структуризацию решения, что довольно удобно для решения учащимися и облегчает работу с решениями при автоматизации расчетов, например, при помощи ПК, потому что решение “в виде уравнения” более просто обрабатывать, чем решение “в виде неравенства”. Метод даёт ответ на вопрос не только, где выполняется требуемое неравенство, но и на сколько левая часть неравенства отличается от правой.

2. Данный метод дает возможность обобщить понятие неравенства, рассматривая задачу его решения как поиск образа по данным прообразу и закону отображения.

3. Обобщенный подход практически нужен, например, для расшифровки фотоснимков, сделанных с орбит искусственных спутников Земли и аэрофотосъемки: отображением является проектирование ( проективное отображение). Фактически, мы всегда делаем этот поиск, представляя объект по его изображению на экране телевизора, на фото и т.д. Только мы это делаем на качественном уровне, а в этой работе мы выполняем и количественный анализ, указывая прообраз каждой точки, которая помечена двумя параметрами ( r , у ⁰ ). Один из них – число r , а другой – точка у ⁰ на единичной сфере в пространстве Y . Для класических неравенств   f ( x ) > 0 это только число r , а точка – число +1 ; для неравенств   f ( x ) < 0 точкой является число –1 . Единичная сфера тут –   концы отрезка        [–1;+1]. Для комплекснозначной функции этой сферой является окружность | х | = 1. Для пространства R ³ имеем собственно сферу радиуса 1 с центром в т. О( 0,0,0 ) . Вектор у ⁰ можно задать в сферических координатах ( 1, j , q ).

4. Введение в неравенство переменного параметра t вводит в задачу движение. Это позволяет определять и скорость х ? ( t ) движ ения по линии х ( t ).

Автор признателен своему ученику С.П. Ткаченко за проверку выкладок и построение рисунка. Им разработаны программы, позволяющие автоматизировать вычисления и построение множеств - решений.

Список литературы:

1. Філер З.Ю. Рівняння та нерівності в науці та навчанні // Математика, її застосування та викладання . Матер. міжвуз . регіон . конф . (24 - 25.09.1999 р.). – Кіровоград : КДПУ . – С. 141-145.

2. Филер З.Е., Ткаченко С.П. Комплексные решения квадратного неравенства // Понтрягинские чтения – ХI . Тезисы докл . – Воронеж: ВГУ , 2000. – С. 142.

3. Ткаченко С.П., Філер З.Ю. Комплексні розв’язки квадратної нерівності // Математика в школі , 2003, № 2. – С. 47-49.

4.   Ткаченко С.П. ,   Філер З.Ю.. Спосіб нев’язки ( відхилу ) розв’язування нерівності // Теорія та методика навчання математики, фізики , інформатики : Збірник наукових праць . Матер. всеукр . наук.-метод . конф . ( 13-14.03.2003р .). Випуск 3: В 3-х томах. – Т. 1: Теорія та методика навчання математики. – Кривий Ріг : Видавничий відділ НМетАУ , 2003. – С.   254-258.