Наши конференции
В данной секции Вы можете ознакомиться с материалами наших конференций
II МНПК "Спецпроект: анализ научных исследований"
II МНПК"Альянск наук: ученый ученому"
I Всеукраинская НПК"Образовательный процесс: взгляд изнутри"
II НПК"Социально-экономические реформы в контексте европейского выбора Украины"
III МНПК "Наука в информационном пространстве"
III МНПК "Спецпроект: анализ научных исследований"
I МНПК "Качество экономического развития"
III МНПК "Альянс наук: ученый- ученому"
IV МНПК "Социально-экономические реформы в контексте интеграционного выбора Украины"
I МНПК "Проблемы формирования новой экономики ХХI века"
IV МНПК "Наука в информационном пространстве"
II МНПК "Проблемы формирования новой экономики ХХI века"
I НПК "Язык и межкультурная коммуникация"
V МНПК "Наука в информационном пространстве"
II МНПК "Качество экономического развития"
IV МНПК "Спецпроект: анализ научных исследований"
ІІІ НПК "Образовательный процесс: взгляд изнутри"
VI МНПК "Социально-экономические реформы в контексте интеграционного выбора Украины"
МНПК «Проблемы формирования новой экономики ХХI века»
IV МНПК "Образовательный процесс: взгляд изнутри"
IV МНПК "Современные проблемы инновационного развития государства"
VI МНПК «Наука в информационном пространстве»
IV МНПК "Проблемы формирования новой экономики ХХI века"
II МНПК студентов, аспирантов и молодых ученых "ДЕНЬ НАУКИ"
VII МНРК "Социально-экономические реформы в контексте интеграционного выбора Украины"
VI МНПК "Спецпроект: анализ научных исследований"
VII МНПК "Наука в информационном пространстве"
II МНК "Теоретические и прикладные вопросы филологии"
VII МНПК "АЛЬЯНС НАУК: ученый - ученому"
IV МНПК "КАЧЕСТВО ЭКОНОМИЧЕСКОГО РАЗВИТИЯ: глобальные и локальные аспекты"
I МНПК «Финансовый механизм решения глобальных проблем: предотвращение экономических кризисов»
I Международная научно-практическая Интернет-конференция «Актуальные вопросы повышения конкурентоспособности государства, бизнеса и образования в современных экономических условиях»(Полтава, 14?15 февраля 2013г.)
I Международная научно-практическая конференция «Лингвокогнитология и языковые структуры» (Днепропетровск, 14-15 февраля 2013г.)
Региональная научно-методическая конференция для студентов, аспирантов, молодых учёных «Язык и мир: современные тенденции преподавания иностранных языков в высшей школе» (Днепродзержинск, 20-21 февраля 2013г.)
IV Международная научно-практическая конференция молодых ученых и студентов «Стратегия экономического развития стран в условиях глобализации» (Днепропетровск, 15-16 марта 2013г.)
VIII Международная научно-практическая Интернет-конференция «Альянс наук: ученый – ученому» (28–29 марта 2013г.)
Региональная студенческая научно-практическая конференция «Актуальные исследования в сфере социально-экономических, технических и естественных наук и новейших технологий» (Днепропетровск, 4?5 апреля 2013г.)
V Международная научно-практическая конференция «Проблемы и пути совершенствования экономического механизма предпринимательской деятельности» (Желтые Воды, 4?5 апреля 2013г.)
Всеукраинская научно-практическая конференция «Научно-методические подходы к преподаванию управленческих дисциплин в контексте требований рынка труда» (Днепропетровск, 11-12 апреля 2013г.)
VІ Всеукраинская научно-методическая конференция «Восточные славяне: история, язык, культура, перевод» (Днепродзержинск, 17-18 апреля 2013г.)
VIII Международная научно-практическая Интернет-конференция «Спецпроект: анализ научных исследований» (30–31 мая 2013г.)
Всеукраинская научно-практическая конференция «Актуальные проблемы преподавания иностранных языков для профессионального общения» (Днепропетровск, 7–8 июня 2013г.)
V Международная научно-практическая Интернет-конференция «Качество экономического развития: глобальные и локальные аспекты» (17–18 июня 2013г.)
IX Международная научно-практическая конференция «Наука в информационном пространстве» (10–11 октября 2013г.)
ДОВЕДЕННЯ НЕЗАЛЕЖНОСТІ СИСТЕМИ АКСІОМ ПЕАНО
Л. О. Іваненко
Постановка проблеми. Аксіоматичний метод – один із методів побудови і дослідження математичних теорій сучасності. Його розвиток починається з Давньої Греції, а продовжується і в наші дні.
Подальший розвиток цього методу є досить важливим. Адже він є найбільш економним, а також більш чітко виявляє структуру математичних теорій, допомагає розв’язати проблеми, які не вирішуються при звичайному змістовному їх тлумаченні.
У формальному плані система аксіом повинна бути несуперечливою, повною та незалежною. Щоб бути впевненим у надійності обраної системи аксіом потрібно мати такі об’єкти, які можуть бути точною інтерпретацією цієї системи аксіом.
Аналіз літератури. В наш час досить багато робіт присвячено аксіоматичному методу в математиці. Зокрема досить детально розглядається питання незалежності системи аксіом. Хоча питання доведення незалежності системи аксіом Пеано зустрічається в різній літературі, зокрема в підручниках Вивальнюка Л. М. Числові системи, Нечаев В. И. Числовые системи , але в них розглядається доведення незалежності лише перших трьох аксіом.
Мета статті. Доведення незалежності всіх аксіом Пеано .
Доведення незалежності аксіом Пеано.
Н езалежність аксіоми n 1 .
- ?
Доведення .
Розглянемо алгебру (А
1
, ', +,
1) , А
1
= {
,
,
}, в якій операції слідування ( ' ) , додавання (+) і множення (
) означені так:
1)
2)
3)
В алгебрі А
1
не виконується аксіома
n
1
, бо в н ій кожний елемент, у тому числі й одиничний елемент
, має передуючий. Решта шість аксіом Пеано в
А
1
виконується(справджується). Це можна перевірити безпосередньо, бо множина А
1
= {
,
,
} містить тільки три елементи. Таким чином, алгебра
А
1
буде моделлю для системи аксіом
n
2
–
n
7
. Цим незалежність
n
1
від решти аксіом доведено.
Н езалежність аксіоми n 2 .
Доведення.
Щоб довести незалежність аксіоми
n
2
від решти аксіом
n
1
,
n
3
–
n
7
, розглянемо алгебру (А
1
, ',+,
1),А
1
= {
,
,
,
}, в якій операції ', + ,
означені так:
1)
2)
3)
В алгебрі А
2
не виконується аксіома
n
2
, бо
, але
(тут елемент 2 йде за двома елементами : 1 і 4). Проте решта аксіом Пеано в А
2
виконуються .
Доведемо незалежність аксіоми n 3 .
Доведення .
Розглянемо алгебру (А
3
;
,
,
, (1,1)), А
3
= {
}, а відповідні операції визначаються так:
1)
2)
3)
Елемент (1, 1) беремо за одиницю . Легко впевнитися , що в алгебрі А
3
виконуються всі аксіоми Пеано, крім аксіоми
n
3
. Аксіома
n
3
не виконується . Справді , нехай
де
Тоді (1,1)
, тобто умови аксіоми
n
3
виконуються , а наслідок не виконується , бо
[ 1 ]
Доведемо незалежність аксіоми n 4 .
- ?
Доведення .
Розглянемо алгебру (А
4
;+ ,
, ', 1 ).
А
4
= N , в якій операції слідування ', додавання + і множення
о значаються так:
,
,
,
,
…
|
? |
1 |
2 |
3 |
4 |
… |
|
1 |
1 |
2 |
3 |
4 |
|
|
2 |
2 |
3 |
5 |
7 |
|
|
3 |
3 |
5 |
7 |
8 |
|
|
4 |
4 |
7 |
8 |
1 1 |
|
|
… |
|
|
|
|
|
|
+ |
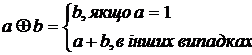
1 |
2 |
3 |
4 |
… |
|
1 |
1 |
2 |
3 |
4 |
|
|
2 |
2 |
3 |
4 |
5 |
|
|
3 |
3 |
4 |
5 |
6 |
|
|
4 |
4 |
5 |
6 |
7 |
|
|
… |
|
|
|
|
|
В алгебрі А 4 не виконується аксіома n 4 , так як 1+1=1, що неможливо . Решта аксіом Пеано в А 4 виконуються .
Доведемо незалежність аксіоми n 5 .
-?
Доведення .
Розглянемо алгебру (А
5
;+ ,
, ', 1 ).
А
5
= N , в якій операції слідування ', додавання + і множення
о значаються так:
,
,
,
,
…
|
? |
1 |
2 |
3 |
4 |
… |
|
1 |
1 |
2 |
3 |
4 |
|
|
2 |
2 |
3 |
5 |
7 |
|
|
3 |
3 |
5 |
8 |
1 1 |
|
|
4 |
4 |
7 |
1 1 |
1 5 |
|
|
… |
|
|
|
|
|
|
+ |
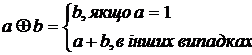
1 |
2 |
3 |
4 |
… |
|
1 |
2 |
3 |
4 |
5 |
|
|
2 |
3 |
3 |
5 |
6 |
|
|
3 |
4 |
5 |
6 |
7 |
|
|
4 |
5 |
6 |
7 |
8 |
|
|
… |
|
|
|
|
|
В алгебрі А
5
не виконується аксіома
n
5
, так як 3=2+2=2+
, ми прийшли до протиріччя . Решта аксіом Пеано в А
5
виконуються .
Доведемо незалежність аксіоми n 6 .
-?
Доведення .
Розглянемо алгебру (А
6
;+ ,
, ', 1 ).
А
6
= N , в якій операції слідування ', додавання + і множення
о значаються так:
,
,
,
,
…
|
+ |
1 |
2 |
3 |
4 |
… |
|
1 |
2 |
3 |
4 |
5 |
|
|
2 |
3 |
4 |
5 |
8 |
|
|
3 |
4 |
5 |
6 |
7 |
|
|
4 |
5 |
8 |
7 |
8 |
|
|
… |
|
|
|
|
|
|
. |
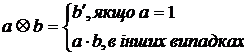
1 |
2 |
3 |
4 |
… |
|
1 |
2 |
3 |
4 |
5 |
|
|
2 |
3 |
5 |
7 |
9 |
|
|
3 |
4 |
7 |
10 |
13 |
|
|
4 |
5 |
9 |
13 |
17 |
|
|
… |
|
|
|
|
|
В алгебрі А
6
не виконується аксіома
n
6
, так як
, що неможливо . Решта аксіом Пеано в А
6
виконуються .
Доведемо незалежність аксіоми n 7 .
-?
Доведення .
Розглянемо алгебру (А
7
;+ ,
, ', 1 ).
А
7
= N , в якій операції слідування ', додавання + і множення
визначаються так:
,
,
,
,
…
|
+ |
1 |
2 |
3 |
4 |
… |
|
1 |
2 |
3 |
4 |
5 |
|
|
2 |
3 |
4 |
5 |
6 |
|
|
3 |
4 |
5 |
6 |
7 |
|
|
4 |
5 |
6 |
7 |
8 |
|
|
… |
|
|
|
|
|
|
. |
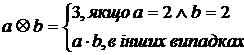
1 |
2 |
3 |
4 |
… |
|
1 |
1 |
2 |
3 |
4 |
|
|
2 |
2 |
3 |
5 |
7 |
|
|
3 |
3 |
5 |
8 |
1 1 |
|
|
4 |
4 |
7 |
1 1 |
1 5 |
|
|
… |
|
|
|
|
|
В алгебрі А
7
не виконується аксіома
n
7
, так як
, ми прийшли до протиріччя . Решта аксіом Пеано в А
7
виконуються .
Висновок. Таким чином, доведено незалежність всіх аксіом Пеано . Розглянуто доцільність застосування аксіоматичного методу.
Література:
1. Вивальнюк Л. М. Числові системи. – К.: Вища школа, 1977. – 184с.
